 wobei S = pd2/4 die projizierte Fläche des Körpers darstellt. ?Ud/ľ ist die Reynolds´sche Zahl Re und das Geschwindigkeitsverhältnis v/U stellt den Spin-Parameter dar. Während eines typischen Golfschlags werden sich sowohl Re-Zahl, als auch der Spin-Parameter ändern, folglich also auch Auftriebs- und Widerstandsbeiwert variieren. Der Spin-Parameter wird in etwa 0,1 betragen, wenn die anfängliche Rotation ungefähr 3500 U/min beträgt. Während des Fluges wird die Geschwindigkeit des Balles sinken und sich somit die Re-Zahl reduzieren. Der Spin-Parameter wird sich trotz Abnahme der Spin-Rate erhöhen. Der etwas kleinere britische Golfball, mit einem Durchmesser von 41,1 mm und einer angenommenen Anfangsgeschwindigkeit von 75 m/s vom Abschlag besitzt eine zugehörige Re-Zahl von ungefähr 2,1ˇ105.
wobei S = pd2/4 die projizierte Fläche des Körpers darstellt. ?Ud/ľ ist die Reynolds´sche Zahl Re und das Geschwindigkeitsverhältnis v/U stellt den Spin-Parameter dar. Während eines typischen Golfschlags werden sich sowohl Re-Zahl, als auch der Spin-Parameter ändern, folglich also auch Auftriebs- und Widerstandsbeiwert variieren. Der Spin-Parameter wird in etwa 0,1 betragen, wenn die anfängliche Rotation ungefähr 3500 U/min beträgt. Während des Fluges wird die Geschwindigkeit des Balles sinken und sich somit die Re-Zahl reduzieren. Der Spin-Parameter wird sich trotz Abnahme der Spin-Rate erhöhen. Der etwas kleinere britische Golfball, mit einem Durchmesser von 41,1 mm und einer angenommenen Anfangsgeschwindigkeit von 75 m/s vom Abschlag besitzt eine zugehörige Re-Zahl von ungefähr 2,1ˇ105.
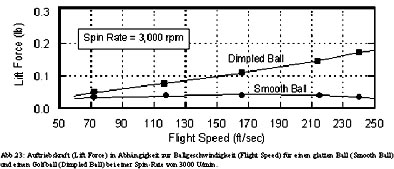
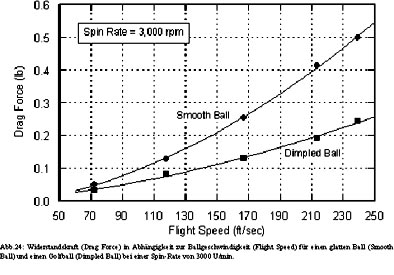
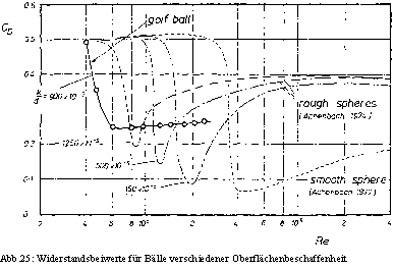 Abbildung 25 zeigt die zugehörigen Widerstandswerte für zunehmende Re-Zahlen für einen Ball mit glatter Oberfläche, jeweils drei mit aufgerauter Oberfläche und einem Golfball mit den obligatorischen Dimples. Eine mit Sandpapier aufgeraute Oberfläche setzt die kritische Re-Zahl herab und lässt die Kurven, etwas getrennt von der feinsten Aufrauung, steigen und bei einem CD-Wert von 0,4 wieder zusammenlaufen. So lässt sich zeigen, dass ein Golfball mit Dimples weniger Widerstand als ein glatter Ball produziert. Dimples weisen jedoch eine sehr grobe Aufrauung auf und es ist zweifelhaft, ob man sie mit einer derart aufgerauten Oberfläche vergleichen kann.
Abbildung 25 zeigt die zugehörigen Widerstandswerte für zunehmende Re-Zahlen für einen Ball mit glatter Oberfläche, jeweils drei mit aufgerauter Oberfläche und einem Golfball mit den obligatorischen Dimples. Eine mit Sandpapier aufgeraute Oberfläche setzt die kritische Re-Zahl herab und lässt die Kurven, etwas getrennt von der feinsten Aufrauung, steigen und bei einem CD-Wert von 0,4 wieder zusammenlaufen. So lässt sich zeigen, dass ein Golfball mit Dimples weniger Widerstand als ein glatter Ball produziert. Dimples weisen jedoch eine sehr grobe Aufrauung auf und es ist zweifelhaft, ob man sie mit einer derart aufgerauten Oberfläche vergleichen kann.
Definitionen: L Auftrieb; D Widerstand; CL Auftriebsbeiwert; CD Widerstandsbeiwert; ? Dichte der Luft; ľ Viskosität der Luft; N Rotationsgeschwindigkeit; U Geschwindigkeit durch die Luft; d Durchmesser; v Oberflächengeschwindigkeit = pNd/60; Re Reynolds´sche Zahl; S Querschnittsfläche des Balles = pd2/4; k durchschnittlicher Sandkorn-Durchmesser;
von J. Maccoll und J. M. Davies
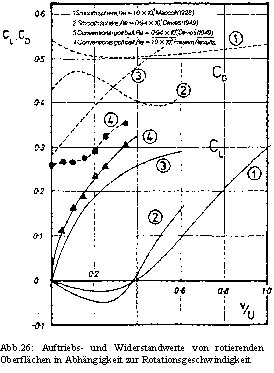 Daten über aerodynamische Kräfte von rotierenden Körpern, deren Rotationsachse horizontal und rechtwinklig zur Flugrichtung zeigt, sind sehr selten. Abbildung 26 zeigt Messungen im Windkanal von Maccoll und Davies. Hier werden CD und CL gegenüber dem Spin Parameter v/U bei einer Re-Zahl von etwa 105 aufgezeigt. Die Fälle 1 und 2 gelten für eine glatte Oberfläche, wobei Fall 3 die Kräfte eines konventionellen Golfballes aufzeigt. Davies benutzte eine Vorrichtung, in der der Ball mit Hilfe zweier Halbschalen zum Rotieren gebracht wurde und anschließend in den Luftstrom losgelassen wurde. Durch das Notieren der Distanz, die der Ball durch den Luftstrom zurückgelegt hatte, konnte er auf die aerodynamischen Kräfte schließen. Maccoll erreichte eine Drehung seines Balles durch eine Spindel, an der der Ball montiert war, die einem Durchmesser von etwa 15% im Vergleich zu dem des Balles besaß. Eine Ausnahme von Davies Arbeit war, dass die Re-Zahl 9,4ˇ104 betrug, was etwas weniger ist, als der Wert, der ungefähr für einen geschlagenen Ball gilt. Das Hauptziel der Untersuchungen war, Auftriebs- und Widerstandskräfte im Windkanal zu messen, um die Flugbahn vorherzubestimmen. Die Weiten dieser vorausgesagten Flugbahnen können dann mit realen Messungen von Golfschlägen unter kontrollierten Bedingungen verglichen werden. Ein anderer Grund dieser Versuchungen war, die Auswirkungen auf die Kräfte bei Veränderung der Dimple-Form zu erforschen.
Die Kräfte auf einen konventionellen Golfball mit runden Dimples wurden mit denen eines Uniroyal Plus 6 verglichen. Der Plus 6 weist eine andere Dimple-Form auf, er besitzt 240 fünfeckige Dimples, die alle in gleichseitigen Dreiecken auf der Oberfläche angeordnet sind. Die Hersteller sagen, dass der Plus 6, nachfolgend Ball mit sechseckigen Dimples genannt, in den meisten Fällen bei gleicher Anfangsgeschwindigkeit, gleichem Spin und Startwinkel höhere Weiten erreicht.
Daten über aerodynamische Kräfte von rotierenden Körpern, deren Rotationsachse horizontal und rechtwinklig zur Flugrichtung zeigt, sind sehr selten. Abbildung 26 zeigt Messungen im Windkanal von Maccoll und Davies. Hier werden CD und CL gegenüber dem Spin Parameter v/U bei einer Re-Zahl von etwa 105 aufgezeigt. Die Fälle 1 und 2 gelten für eine glatte Oberfläche, wobei Fall 3 die Kräfte eines konventionellen Golfballes aufzeigt. Davies benutzte eine Vorrichtung, in der der Ball mit Hilfe zweier Halbschalen zum Rotieren gebracht wurde und anschließend in den Luftstrom losgelassen wurde. Durch das Notieren der Distanz, die der Ball durch den Luftstrom zurückgelegt hatte, konnte er auf die aerodynamischen Kräfte schließen. Maccoll erreichte eine Drehung seines Balles durch eine Spindel, an der der Ball montiert war, die einem Durchmesser von etwa 15% im Vergleich zu dem des Balles besaß. Eine Ausnahme von Davies Arbeit war, dass die Re-Zahl 9,4ˇ104 betrug, was etwas weniger ist, als der Wert, der ungefähr für einen geschlagenen Ball gilt. Das Hauptziel der Untersuchungen war, Auftriebs- und Widerstandskräfte im Windkanal zu messen, um die Flugbahn vorherzubestimmen. Die Weiten dieser vorausgesagten Flugbahnen können dann mit realen Messungen von Golfschlägen unter kontrollierten Bedingungen verglichen werden. Ein anderer Grund dieser Versuchungen war, die Auswirkungen auf die Kräfte bei Veränderung der Dimple-Form zu erforschen.
Die Kräfte auf einen konventionellen Golfball mit runden Dimples wurden mit denen eines Uniroyal Plus 6 verglichen. Der Plus 6 weist eine andere Dimple-Form auf, er besitzt 240 fünfeckige Dimples, die alle in gleichseitigen Dreiecken auf der Oberfläche angeordnet sind. Die Hersteller sagen, dass der Plus 6, nachfolgend Ball mit sechseckigen Dimples genannt, in den meisten Fällen bei gleicher Anfangsgeschwindigkeit, gleichem Spin und Startwinkel höhere Weiten erreicht.Es wurden drei Windkanal-Modelle angefertigt: Eines, mit den Eigenschaften eines konventionellen Golfballs, ein Modell mit sechseckigen Dimples und eines mit glatter Oberfläche. Jedes Modell bestand aus einer hohlen Schale, die halbiert wurde, um einen kleinen Motor und zwei Kugellager unterzubringen, um die das Modell rotierte.
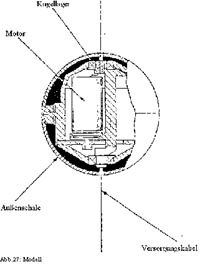 Die Details sind in Abbildung 27 gezeigt. Das Modell wird im Windkanal an einem 0,50 mm dicken Kabel aufgehängt und gleichermaßen unten an einem Kabel von 0,20 mm Durchmesser befestigt, um eine vertikale Rotationsachse zu gewährleisten. Der Durchmesser des dicksten Kabels betrug nur etwa 0,5% des Durchmessers des Balles. Auch wurden diese Kabel für die Stromversorgung des Motors benutzt. Das obere Kabel wird außerdem an einem beweglichen Messarm befestigt, um die Auftriebskraft des Balles (wobei es sich bei einer vertikalen Rotations-achse um eine seitliche Kraft handelt) zu messen. Der Messarm und sonstige Mess- und Befestigungsvorrichtungen wurden durch Stromlinienförmige Verkleidungen vom Luftstrom abgeschirmt. Der Widerstand der freiliegenden Kabel wurde vom Gesamtwiderstand subtrahiert. Die Rotationsgeschwindigkeit wurde mit Hilfe eines Stroboskops gemessen.
Die Details sind in Abbildung 27 gezeigt. Das Modell wird im Windkanal an einem 0,50 mm dicken Kabel aufgehängt und gleichermaßen unten an einem Kabel von 0,20 mm Durchmesser befestigt, um eine vertikale Rotationsachse zu gewährleisten. Der Durchmesser des dicksten Kabels betrug nur etwa 0,5% des Durchmessers des Balles. Auch wurden diese Kabel für die Stromversorgung des Motors benutzt. Das obere Kabel wird außerdem an einem beweglichen Messarm befestigt, um die Auftriebskraft des Balles (wobei es sich bei einer vertikalen Rotations-achse um eine seitliche Kraft handelt) zu messen. Der Messarm und sonstige Mess- und Befestigungsvorrichtungen wurden durch Stromlinienförmige Verkleidungen vom Luftstrom abgeschirmt. Der Widerstand der freiliegenden Kabel wurde vom Gesamtwiderstand subtrahiert. Die Rotationsgeschwindigkeit wurde mit Hilfe eines Stroboskops gemessen.
Am Anfang wird der CD-Wert für einen glatten, nicht rotierenden Ball gemessen, um zu ermitteln, inwieweit die Mess- und Befestigungsvorrichtungen die Messungen verfälschen. Es ist nämlich bekannt, dass die Strömung um einen glatten Körper stark von der Re-Zahl abhängt und schon eine kleine Änderung der Re-Zahl um etwa 4ˇ105 den CD-Wert von 0,45 auf etwa 0,1 reduziert.
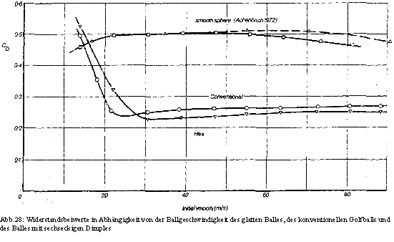 Im hohen CD-Bereich ist die Strömung laminar. Die kritische Re-Zahl, das ist der Wert, ab dem ein starker Abfall des CD-Wertes eingeleitet wird und laminare in turbulente Strömung umschlägt, wird eher eintreten, wenn die Oberfläche aufgeraut ist, oder wenn der entgegenkommende Luftstrom bereits turbulent ist. So wurde angenommen, dass, wenn die Mess- und Befestigungsvorrichtungen den Luftstrom allzu sehr stören, kleine Regionen mit unterbrochenen Strömungen entstehen können, den CD-Wert reduzieren und somit die Messergebnisse nicht mehr mit der Wirklichkeit übereinstimmen. Die Messergebnisse für einen glatten Ball, für den Ball mit konventioneller Dimple-Form und für den mit sechseckigen Dimples, sind in Abbildung 28 in Abhängigkeit von der Anfangsgeschwindigkeit eingezeichnet. Man kann erkennen, dass der glatte Ball durchwegs einen hohen Widerstandsbeiwert aufweist.
Im hohen CD-Bereich ist die Strömung laminar. Die kritische Re-Zahl, das ist der Wert, ab dem ein starker Abfall des CD-Wertes eingeleitet wird und laminare in turbulente Strömung umschlägt, wird eher eintreten, wenn die Oberfläche aufgeraut ist, oder wenn der entgegenkommende Luftstrom bereits turbulent ist. So wurde angenommen, dass, wenn die Mess- und Befestigungsvorrichtungen den Luftstrom allzu sehr stören, kleine Regionen mit unterbrochenen Strömungen entstehen können, den CD-Wert reduzieren und somit die Messergebnisse nicht mehr mit der Wirklichkeit übereinstimmen. Die Messergebnisse für einen glatten Ball, für den Ball mit konventioneller Dimple-Form und für den mit sechseckigen Dimples, sind in Abbildung 28 in Abhängigkeit von der Anfangsgeschwindigkeit eingezeichnet. Man kann erkennen, dass der glatte Ball durchwegs einen hohen Widerstandsbeiwert aufweist.
Man sieht, dass die Messergebnisse für den Ball mit glatter Oberfläche gut mit Werten von Achenbach übereinstimmen, sie liegen auch innerhalb der Streuung bisher veröffentlichter Daten. Die beiden Kurven der Bälle mit Dimples zeigen deutlich die kritische Re-Zahl, und obwohl die Reduktion des CD-Wertes geringer als bei einem Ball mit glatter Oberfläche ist, geschieht dieser Umschlag von laminarer auf turbulente Strömung (= kritische Re-Zahl) bereits bei einem geringen Wert (siehe Abbildung 25). Bei Geschwindigkeiten ab 30 m/s besitzt der Ball mit den sechseckigen Dimples einen niedrigeren Widerstands-beiwert als ein konventioneller Ball.
Nun ist es interessant, die Widerstandsbeiwerte eines normalen Golfballes mit den eines Balles dessen Oberfläche mit Sandpapier aufgeraut wurde bei unterschiedlichen Re-Zahlen zu vergleichen. Achenbach hat dazu zahlreiche Messungen durchgeführt und dabei das Verhältnis der Durchschnittsdurchmesser der Sandkörner und des Durchmessers des Körpers variiert. Seine Ergebnisse werden in Abbildung 26 gezeigt. Man sieht, dass bei Zunahme von k/d (d.h. Zunahme des durchschnittlichen Sandkorn-Durchmessers) der Wert der kritischen Re-Zahl abnimmt, jedoch nach einem Minimum der CD-Wert wieder rasch zunimmt. Es ist schwierig, Dimples mit einer durch Sandpapier aufgerauten Oberfläche zu vergleichen, aber vermutlicherweise ist das Verhältnis der Dimple-Tiefe zum Balldurchmesser (i.e. k/d = 900ˇ10-5) ein relevanter Parameter. Wenn man aber die Widerstandsbeiwerte der Golfbälle mit denen der durch Sandpapier aufgerauten Bälle vergleicht, scheinen Dimples beim gleichem Verhältnis von k/d effektiver zu sein und den Wert der kritischen Re-Zahl herabzusetzen. Eine andere interessante Tatsache ist, dass beim Golfball keine erneute Zunahme des CD-Wertes nach einem bestimmten Punkt zu beobachten ist. Daraus folgt, dass die Strömungen um die Dimples und die Form der Dimples wichtig für die Bestimmung des CD-Wertes sein müssen.
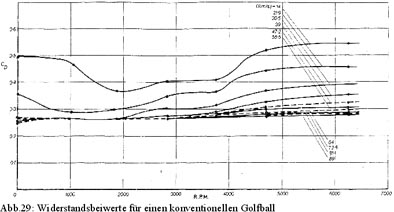
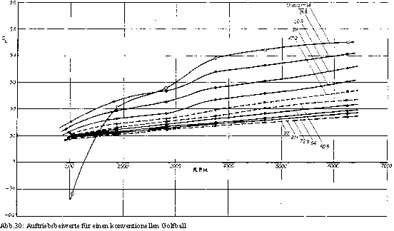
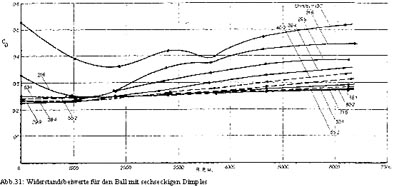
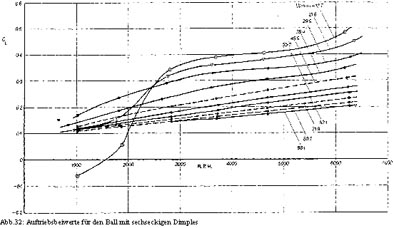 Für die beiden Bälle mit unterschiedlicher Dimple-Form wurden Messungen für zehn verschiedene Geschwindigkeiten und Spins bis zu 6250 U/min durchgeführt. Das liefert eine Menge an Werten für beide Bälle mit einem großen Bereich an Re-Zahlen und Spin-Parametern. Die Variationen von Widerstands- und Auftriebsbeiwert des rotierenden Golfballs mit den runden Dimples für zehn verschiedene Geschwindigkeiten, sind in Abbildung 29 und 30 gezeigt. Die entsprechenden Werte für den Golfball mit sechseckigen Dimples finden sich in Abbildung 31 und 32. Wenn man den Einfluss der sich ändernden Re-Zahl unberücksichtigt lässt, nimmt man an, dass der Auftriebsbeiwert bei größerem Spin zunimmt und dass gleichermaßen der Widerstands-Effekt dadurch erhöht wird und CD ansteigen lässt. Belässt man die Umdrehungszahl pro Minute unverändert, bewirkt die Zunahme der Geschwindigkeit ein Fallen des Faktors v/U und die Abnahme der beiden Beiwerte CD und CL. Genau dies zeigen die Abbildungen 29 bis 32, wobei die Messungen für niedrige Umdrehungszahlen bei niedriger Geschwindigkeit etwas aus dem Rahmen fallen. Es scheint, dass der Auftrieb in den Abbildungen 30 und 32 bei einer Spin-Rate unter 1500 U/min negativ ist. Das liegt daran, dass bei minimaler Geschwindigkeit die Re-Zahl unterhalb des kritischen Wertes und die Strömung um den nicht rotierenden Ball laminar ist. Dreht sich der Ball, treten Störungen zuerst in der Grenzschicht unmittelbar auf der Balloberfläche auf und wandern entlang der Oberfläche auf die Kehrseite, die sich gegen den Hauptstrom bewegt, bei Backspin also auf die Unterseite des Balles. Auf dieser Seite tritt nun die Veränderung auf, die einen negativen Auftrieb hervorruft. Bei weiterem Ansteigen der Spin-Rate und der Geschwindigkeit, treten ebenfalls Störungen auf der Oberseite des Balles auf, die den Auftrieb nun in einen positiven umwandeln. Dies ist nun der kritische Punkt der Re-Zahl, an dem die laminaren in turbulente Strömungen übergehen. Überhalb der kritischen Re-Zahl bewirkt eine Erhöhung der Rotationsgeschwindigkeit einen nahezu linearen Anstieg des Auftriebs. Das nicht lineare Verhalten bis 1000 U/min bedeutet, dass der Auftrieb nicht anhand einer einfachen Stromfluss-Theorie erklärt werden kann.
Für die beiden Bälle mit unterschiedlicher Dimple-Form wurden Messungen für zehn verschiedene Geschwindigkeiten und Spins bis zu 6250 U/min durchgeführt. Das liefert eine Menge an Werten für beide Bälle mit einem großen Bereich an Re-Zahlen und Spin-Parametern. Die Variationen von Widerstands- und Auftriebsbeiwert des rotierenden Golfballs mit den runden Dimples für zehn verschiedene Geschwindigkeiten, sind in Abbildung 29 und 30 gezeigt. Die entsprechenden Werte für den Golfball mit sechseckigen Dimples finden sich in Abbildung 31 und 32. Wenn man den Einfluss der sich ändernden Re-Zahl unberücksichtigt lässt, nimmt man an, dass der Auftriebsbeiwert bei größerem Spin zunimmt und dass gleichermaßen der Widerstands-Effekt dadurch erhöht wird und CD ansteigen lässt. Belässt man die Umdrehungszahl pro Minute unverändert, bewirkt die Zunahme der Geschwindigkeit ein Fallen des Faktors v/U und die Abnahme der beiden Beiwerte CD und CL. Genau dies zeigen die Abbildungen 29 bis 32, wobei die Messungen für niedrige Umdrehungszahlen bei niedriger Geschwindigkeit etwas aus dem Rahmen fallen. Es scheint, dass der Auftrieb in den Abbildungen 30 und 32 bei einer Spin-Rate unter 1500 U/min negativ ist. Das liegt daran, dass bei minimaler Geschwindigkeit die Re-Zahl unterhalb des kritischen Wertes und die Strömung um den nicht rotierenden Ball laminar ist. Dreht sich der Ball, treten Störungen zuerst in der Grenzschicht unmittelbar auf der Balloberfläche auf und wandern entlang der Oberfläche auf die Kehrseite, die sich gegen den Hauptstrom bewegt, bei Backspin also auf die Unterseite des Balles. Auf dieser Seite tritt nun die Veränderung auf, die einen negativen Auftrieb hervorruft. Bei weiterem Ansteigen der Spin-Rate und der Geschwindigkeit, treten ebenfalls Störungen auf der Oberseite des Balles auf, die den Auftrieb nun in einen positiven umwandeln. Dies ist nun der kritische Punkt der Re-Zahl, an dem die laminaren in turbulente Strömungen übergehen. Überhalb der kritischen Re-Zahl bewirkt eine Erhöhung der Rotationsgeschwindigkeit einen nahezu linearen Anstieg des Auftriebs. Das nicht lineare Verhalten bis 1000 U/min bedeutet, dass der Auftrieb nicht anhand einer einfachen Stromfluss-Theorie erklärt werden kann.
Um den Auftrieb und den Widerstand beider Dimple-Konfigurationen vergleichen zu können, wurden die CL- und CD-Werte in Abhängigkeit von v/U für verschiedene Re-Zahlen in einem gemeinsamen Koordinatensystem eingetragen. Abbildung 33 zeigt die Werte für Re-Zahlen von 1,26ˇ105 bis 2,38ˇ105, was ungefähr Geschwindigkeiten von 45 bis 88 m/s entspricht.
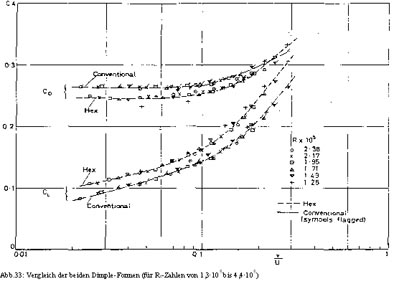 Das Zusammenliegen der Daten verschiedener Messdurchgänge spiegelt die Nichtigkeit der Höhe der Re-Zahl wieder und zeigt außerdem die Geschwindigkeit experimentell bestimmter Ergebnisse. Bei Werten für Re-Zahlen unterhalb von 1,26ˇ105, die hier nicht mehr eingezeichnet wurden, tritt jedoch ein Einfluss dieses Wertes auf die Daten auf und macht eine Zusammenfassung der gesamten Daten in Form einer Universal-Kurve nicht mehr möglich. Im Allgemeinen kann man jedoch sagen, wenn sich der Auftrieb vergrößert, steigt auch der Widerstand. Außerdem ist der Golfball mit den sechseckigen Dimples dem üblichen Golfball überlegen, da er mehr Auftrieb und geringeren Widerstand produziert außer der Überschneidung der CD-Kurven bei hohen v/U-Werten, ab wo der Ball ohnehin verstärkten Auftrieb aufweist.
Das Zusammenliegen der Daten verschiedener Messdurchgänge spiegelt die Nichtigkeit der Höhe der Re-Zahl wieder und zeigt außerdem die Geschwindigkeit experimentell bestimmter Ergebnisse. Bei Werten für Re-Zahlen unterhalb von 1,26ˇ105, die hier nicht mehr eingezeichnet wurden, tritt jedoch ein Einfluss dieses Wertes auf die Daten auf und macht eine Zusammenfassung der gesamten Daten in Form einer Universal-Kurve nicht mehr möglich. Im Allgemeinen kann man jedoch sagen, wenn sich der Auftrieb vergrößert, steigt auch der Widerstand. Außerdem ist der Golfball mit den sechseckigen Dimples dem üblichen Golfball überlegen, da er mehr Auftrieb und geringeren Widerstand produziert außer der Überschneidung der CD-Kurven bei hohen v/U-Werten, ab wo der Ball ohnehin verstärkten Auftrieb aufweist.
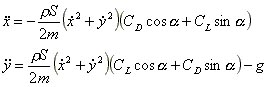 wobei x und y in horizontaler bzw. vertikaler Richtung gemessen werden, g die Fallbeschleunigung, m die Masse des Balles und a die Neigung der Flugbahn zur Horizontalen ist, d.h.:
wobei x und y in horizontaler bzw. vertikaler Richtung gemessen werden, g die Fallbeschleunigung, m die Masse des Balles und a die Neigung der Flugbahn zur Horizontalen ist, d.h.:
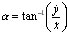 Diese Gleichungen wurden durch ein Schritt-für-Schritt Verfahren mit einem Computer ermittelt. Alle Werte der Windkanal-Versuche wurden im Computer gespeichert und das Programm berechnete zu jedem Zeitpunkt die zugehörigen CL- und CD-Werte. Das Zeitintervall wurde auf 0,001 s festgelegt. Um also die Flugbahn berechnen zu können, müssen zuerst der Anfangsspin, der Abschlagswinkel und die Anfangsgeschwindigkeit bekannt sein. Eine High-Speed Camera wurde verwendet, um diese Daten bei mehreren verschiedenen Golfern zu messen. Die Spieler wurden in zwei Gruppen unterteilt, Professionals und Amateure. Die Testpersonen schlugen mehrere Bälle wobei bei jedem Schlag Abschlagswinkel, Spin und Geschwindigkeit gemessen wurden. Die Durchschnittsergebnisse finden sich in der Tabelle darunter.
Diese Gleichungen wurden durch ein Schritt-für-Schritt Verfahren mit einem Computer ermittelt. Alle Werte der Windkanal-Versuche wurden im Computer gespeichert und das Programm berechnete zu jedem Zeitpunkt die zugehörigen CL- und CD-Werte. Das Zeitintervall wurde auf 0,001 s festgelegt. Um also die Flugbahn berechnen zu können, müssen zuerst der Anfangsspin, der Abschlagswinkel und die Anfangsgeschwindigkeit bekannt sein. Eine High-Speed Camera wurde verwendet, um diese Daten bei mehreren verschiedenen Golfern zu messen. Die Spieler wurden in zwei Gruppen unterteilt, Professionals und Amateure. Die Testpersonen schlugen mehrere Bälle wobei bei jedem Schlag Abschlagswinkel, Spin und Geschwindigkeit gemessen wurden. Die Durchschnittsergebnisse finden sich in der Tabelle darunter.
 Sie zeigt die Daten für einen typischen Treibschlag (Drive), der angewandt wird, um große Weiten zu überwinden. Man erkennt, dass nicht nur die Anfangsgeschwindigkeit, sondern auch der Spin und der Abschlagswinkel der Berufsspieler größer sind.
Sie zeigt die Daten für einen typischen Treibschlag (Drive), der angewandt wird, um große Weiten zu überwinden. Man erkennt, dass nicht nur die Anfangsgeschwindigkeit, sondern auch der Spin und der Abschlagswinkel der Berufsspieler größer sind.
 Eine für einen Treibschlag (Drive) typische Flugbahn ist in Abbildung 34 auf-gezeichnet. Im Ver-lauf der Flugbahn verlieren die Kräfte der Aerodynamik mehr und mehr an Bedeutung, da sowohl die Geschwindigkeit als auch der Spin abnimmt. So wirkt am Ende fast ausschließlich die Gravitationskraft. Dabei ist die Flugbahn des Drives die Unspektakulärste. Aufgrund der relativ geringen Umdrehungszahl des Balles ist diese der Wurfparabel am ähnlichsten. Besitzt der Ball eine wesentlich höhere Umdrehungszahl, ist die Flugkurve sichtlich nach oben gekrümmt, fällt aber dann relativ steil ab. Inwieweit die Rotation nachlässt, kann man nicht genau sagen. Verschiedene Annahmen zum Spin-Verfall, einschließlich der Vermutung, der Verfall sei proportional zum Quadrat der Geschwindigkeit, ergaben jedoch nur sehr geringe Abweichungen. Einige Ergebnisse derBerechnungen zur Abhängigkeit von Spin-Rate, Anfangsgeschwindigkeit und Startwinkel sind in den Abbildungen 35 bis 37 gezeigt.
Eine für einen Treibschlag (Drive) typische Flugbahn ist in Abbildung 34 auf-gezeichnet. Im Ver-lauf der Flugbahn verlieren die Kräfte der Aerodynamik mehr und mehr an Bedeutung, da sowohl die Geschwindigkeit als auch der Spin abnimmt. So wirkt am Ende fast ausschließlich die Gravitationskraft. Dabei ist die Flugbahn des Drives die Unspektakulärste. Aufgrund der relativ geringen Umdrehungszahl des Balles ist diese der Wurfparabel am ähnlichsten. Besitzt der Ball eine wesentlich höhere Umdrehungszahl, ist die Flugkurve sichtlich nach oben gekrümmt, fällt aber dann relativ steil ab. Inwieweit die Rotation nachlässt, kann man nicht genau sagen. Verschiedene Annahmen zum Spin-Verfall, einschließlich der Vermutung, der Verfall sei proportional zum Quadrat der Geschwindigkeit, ergaben jedoch nur sehr geringe Abweichungen. Einige Ergebnisse derBerechnungen zur Abhängigkeit von Spin-Rate, Anfangsgeschwindigkeit und Startwinkel sind in den Abbildungen 35 bis 37 gezeigt.
Abbildung 35 zeigt die Abhängigkeit der Rotation bei einer Anfangsgeschwindigkeit von 58 m/s und einem Abschlagswinkel von 10°. Man sieht, dass bei 4000 U/min ein Maximum an Weite erzielt wird. Verglichen mit einem Schlag ohne Spin (was praktisch nicht möglich ist), weist ein Schlag bei 4000 U/min eine um 90% längere Weite auf. Als Vergleich, kann man der Abbildung ebenfalls entnehmen, dass der Ball ohne Einfluss der aerodynamischen Kräfte (Auftrieb, Widerstand), d.h. im Vakuum und bei sonst gleichen Bedingungen erheblich kürzer fliegt, als mit diesen Kräften. Um zu zeigen, wie entscheidend diese Kräfte sind, ist noch zusätzlich ein Wert für Topspin eingetragen. Ändert sich also das Vorzeichen des Auftriebs, wird die Weite um etwa zwei Drittel reduziert.
Der Effekt bei Veränderung der Geschwindigkeit wird in Abbildung 36 gezeigt. Bei niedrigen Geschwindigkeiten wird auch weniger Auftrieb erzeugt und die Gesamtflugweite ist gering. Ab einer Geschwindigkeit von 30 m/s steigt jedoch die Reichweite rapide, fast linear, an. In der Praxis bewirkt ein schnellerer und kräftigerer Schwung (d.h., eine größere Schlägerkopfgeschwindigkeit) sowohl eine höhere Ballgeschwindigkeit, als auch Spin-Rate. Abbildung 37 zeigt, inwieweit die Flugweite vom Winkel, in dem der Ball den Abschlag verlässt, abhängig ist. Zu bemerken ist, dass diese Kurve nicht durch den Ursprung läuft, da selbst bei 0° der Ball einen Auftrieb erfährt, der ihn einige Meter fliegen lässt. Die Weite steigt stetig, wenn auch langsam, mit dem Winkel bis etwa 15° an. Diese Kurve kann dazu verwendet werden, den Winkel des Schlägerblattes so individuell auf den Spieler anzupassen, dass er maximale Weiten erreicht, da Schlägerkopfgeschwindigkeit und somit die Anfangsgeschwindigkeit des Balles, sowie der Abschlagswinkel und der Spin von Spieler zu Spieler verschieden sind (siehe Tabelle oben).
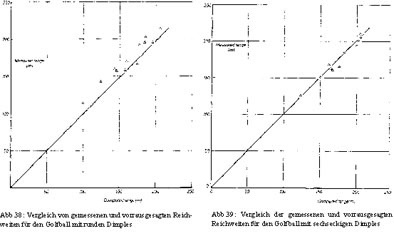
Die letzte Phase der Untersuchungen besteht nun darin, die prophezeiten Weiten aus den Windkanal-Werten mit den wirklichen Ergebnissen einer Abschlagsmaschine zu vergleichen. Bei der Verwendung einer solchen Maschine können die Parameter Geschwindigkeit, Winkel und Spin im Einzelnen kontrolliert und eingestellt werden. Es war jedoch nicht möglich, die gesamte Flugbahn aufzuzeigen, es wurde lediglich der Landepunkt markiert und vermessen. Der Vergleich von gemessenen und errechneten Werten für den konventionellen Ball und dem mit sechseckigen Dimples wird in den Abbildungen 38 und 39 dargestellt. Jeder Wert ist ein Durchschnittswert von insgesamt zehn Bällen, obwohl die Streuung der einzelnen Bälle generell gering war. Die Übereinstimmung der gemessenen und berechneten Werte traten am besten für den Ball mit den sechseckigen Dimples ein, wobei der Golfball mit runden im Allgemeinen etwas weiter flog als berechnet. Dieser Uniroyal Plus 6 mit sechseckigen Dimples erreichte jedoch durchschnittlich bei gleichen Bedingungen um 5,5 m längere Weiten als der Golfball mit der üblichen Dimple-Form.
 Die aerodynamischen Kräfte eines Golfballs hängen von den Strömungen, die in den Dimples entstehen, ab und unglücklicherweise ist es schwierig diese genau zu analysieren, insbesondere, wenn sich der Ball dreht. Klar ist, dass sie Veränderungen bewirken, die den kritischen Wert der Re-Zahl unter den des glatten Balles herabsetzt. Der Unterschied zu den Bällen, deren Oberfläche mit Sandpapier aufgeraut wurde, ist, dass der CD-Wert nicht wieder unmittelbar nach Erreichen der kritischen Re-Zahl steigt. Anscheinend bewirken die Bälle mit aufgerauter Oberfläche, dass die turbulente Grenzschicht dicker wird und somit nicht mehr so nah an die Oberfläche gebunden ist, wogegen die Dimples effektiver wirken. Weiterhin haben Bälle mit sechseckigen Dimples einen Vorteil gegenüber den runden, da sie anscheinend durch ihre Kanten zusätzlich einzelne Wirbel in der Grenzschicht verursachen. Um jedoch mehr Schlüsse ziehen zu können, müsste man die Oberflächenströmungen detailliert untersuchen. Im Endeffekt waren die Vorteile der sechseckigen Dimples nicht so groß wie zuvor bei den Messungen im Windkanal angenommen wurde, da die Weiten des konventionellen Balles etwas unterschätzt wurden. Bis jetzt wurden keine gravierenden Vorteile der sechseckigen Dimples gefunden.
Die aerodynamischen Kräfte eines Golfballs hängen von den Strömungen, die in den Dimples entstehen, ab und unglücklicherweise ist es schwierig diese genau zu analysieren, insbesondere, wenn sich der Ball dreht. Klar ist, dass sie Veränderungen bewirken, die den kritischen Wert der Re-Zahl unter den des glatten Balles herabsetzt. Der Unterschied zu den Bällen, deren Oberfläche mit Sandpapier aufgeraut wurde, ist, dass der CD-Wert nicht wieder unmittelbar nach Erreichen der kritischen Re-Zahl steigt. Anscheinend bewirken die Bälle mit aufgerauter Oberfläche, dass die turbulente Grenzschicht dicker wird und somit nicht mehr so nah an die Oberfläche gebunden ist, wogegen die Dimples effektiver wirken. Weiterhin haben Bälle mit sechseckigen Dimples einen Vorteil gegenüber den runden, da sie anscheinend durch ihre Kanten zusätzlich einzelne Wirbel in der Grenzschicht verursachen. Um jedoch mehr Schlüsse ziehen zu können, müsste man die Oberflächenströmungen detailliert untersuchen. Im Endeffekt waren die Vorteile der sechseckigen Dimples nicht so groß wie zuvor bei den Messungen im Windkanal angenommen wurde, da die Weiten des konventionellen Balles etwas unterschätzt wurden. Bis jetzt wurden keine gravierenden Vorteile der sechseckigen Dimples gefunden.

